What is the fundamental definition and scope of game theory?

Game theory is the study of mathematical models that analyze strategic interactions. It finds extensive application across various fields, including economics, logic, systems science, and computer science, to understand rational decision-making in complex scenarios involving multiple interacting agents.

How did game theory evolve from its early focus on zero-sum games?

Initially, game theory concentrated on two-person zero-sum games, where one participant's gain is precisely the other's loss. By the 1950s, it expanded to encompass non-zero-sum games and was subsequently applied to a broad spectrum of behavioral relationships, becoming a comprehensive science of rational decision-making.

Who are considered the pioneers of modern game theory, and what were their key contributions?

John von Neumann is credited with establishing modern game theory, proving the minimax theorem for two-person zero-sum games. His collaboration with Oskar Morgenstern on "Theory of Games and Economic Behavior" (1944) further developed the field by introducing cooperative games and an axiomatic theory of expected utility, which provided a framework for analyzing decision-making under uncertainty.

What recognition has game theory received in academic fields, particularly regarding Nobel Prizes?

Game theory's significance is highlighted by its recognition through major awards. John Maynard Smith received the Crafoord Prize for evolutionary game theory, and as of 2020, fifteen game theorists have been awarded the Nobel Memorial Prize in Economic Sciences, underscoring the field's impact on economic thought and practice.

What are some of the earliest recorded analyses related to game theory?

Early contributions include Charles Waldegrave's 1713 analysis of the game "le her," which provided a minimax mixed strategy solution, now known as the Waldegrave problem. Later, Antoine Augustin Cournot presented a Nash equilibrium model of oligopoly competition in 1838, and Joseph Bertrand critiqued this model with his own price competition model in 1883.

What significant result did Ernst Zermelo achieve in 1913 concerning games like chess?

In 1913, Ernst Zermelo published a paper demonstrating that the optimal strategy in chess is strictly determined. This groundbreaking work applied set theory to the analysis of games, proving that for games like chess, a definitive optimal strategy exists for one of the players.

How did John von Neumann's work in the 1920s and 1940s lay the groundwork for game theory?

John von Neumann's 1928 paper established game theory as an independent field, using the Brouwer fixed-point theorem to prove the minimax theorem. His 1944 book with Oskar Morgenstern, "Theory of Games and Economic Behavior," expanded this by analyzing cooperative games and developing an axiomatic theory of expected utility, which provided a framework for analyzing decision-making under uncertainty.

What is the significance of the "Theory of Games and Economic Behavior" by von Neumann and Morgenstern?

This seminal 1944 book extended game theory beyond two-person zero-sum games to include cooperative games with multiple players. It also introduced an axiomatic approach to expected utility, providing a mathematical framework for understanding decision-making when outcomes are uncertain.

How did game theory develop significantly in the 1950s?

The 1950s saw a surge in game theory activity, with the development of concepts like the core, extensive form games, fictitious play, repeated games, and the Shapley value. It also began to be applied to philosophy and political science, with RAND Corporation studies exploring its relevance to nuclear strategy.

What is the Nash equilibrium, and who developed it?

The Nash equilibrium, developed by John Nash in 1950, is a solution concept for non-cooperative games. It represents a set of strategies, one for each player, where no player can improve their outcome by unilaterally changing their strategy, assuming all other players keep theirs constant.

Which game theorists were recognized with Nobel Prizes for their contributions to economic game theory?

Several game theorists have received Nobel Prizes in Economic Sciences. Notably, John Nash, Reinhard Selten, and John Harsanyi shared the prize in 1994. Thomas Schelling and Robert Aumann received it in 2005, while Leonid Hurwicz, Eric Maskin, and Roger Myerson were recognized in 2007 for mechanism design theory. Alvin Roth and Lloyd Shapley received the prize in 2012 for stable allocations and market design.

How was game theory applied in biology in the 1970s?

In the 1970s, game theory was extensively applied to biology, largely due to the work of John Maynard Smith. His development of evolutionary game theory and the concept of the evolutionarily stable strategy (ESS) provided a framework for understanding biological evolution and behavior.

What distinguishes cooperative games from non-cooperative games in game theory?

Cooperative games allow players to form binding commitments, often enforced by external mechanisms like contract law. Non-cooperative games, conversely, require agreements to be self-enforcing, relying on credible threats, as players cannot form external alliances.

How do cooperative and non-cooperative game theory approaches differ in their analysis?

Cooperative game theory focuses on predicting coalition formation, joint actions, and collective payoffs, offering a high-level view. Non-cooperative game theory delves deeper into individual player actions and payoffs by analyzing specific equilibria like Nash equilibria, providing a more detailed, generalizable approach.

What defines a symmetric game in game theory?

A symmetric game is one where each player receives the same payoff for choosing a particular strategy, regardless of which player they are. Essentially, the identity of the player does not alter the game's structure or outcomes for others when strategies are identical.

Can a game be asymmetric even if players have identical strategy sets? Provide an example.

Yes, a game can be asymmetric despite having identical strategy sets. The text provides an example of a game depicted in a graphic where the payoffs differ based on player choices, making it asymmetric even though both players have the same options.

What characterizes a zero-sum game?

In a zero-sum game, the total gains and losses among all players sum to zero for every combination of strategies. This means any benefit a player receives comes directly at the expense of other players, with no net change in resources. Poker and chess are cited as examples.

How do non-zero-sum games differ from zero-sum games?

Non-zero-sum games allow for outcomes where the total benefits and losses do not necessarily balance to zero. In these games, a player's gain does not strictly require another player's loss; there can be scenarios where all players benefit or all players lose.

What is the key difference between simultaneous and sequential games?

Simultaneous games involve players making decisions at the same time or without knowledge of each other's moves, often represented by payoff matrices. Sequential games, in contrast, have players making decisions in a specific order, where earlier moves influence subsequent choices, typically visualized using game trees.

How are simultaneous and sequential games typically represented in game theory?

Simultaneous games are commonly represented using normal form, often depicted as payoff matrices. Sequential games are typically represented using extensive form, which visualizes the game's progression as a tree structure, showing the sequence of moves and information available to players.

What defines a game of perfect information?

A game of perfect information is one where all players, at every decision point, are fully aware of the entire history of the game, including all previous moves made by all players. Chess and Go are classic examples of such games.

What is the distinction between perfect information and complete information in game theory?

Perfect information means knowing all past moves. Complete information, a related but distinct concept, refers to players knowing each other's available strategies and payoffs, but not necessarily the specific moves made. Games can have complete information but imperfect information, like many card games.

What is a Bayesian game, and what assumption does it address?

A Bayesian game is a strategic game where players have incomplete information about each other's characteristics, such as their preferences or payoffs. It addresses situations where participants might not fully know their opponents' valuations, costs, or strategies, requiring analysis of players' beliefs about these unknown factors.

What are combinatorial games, and what challenges do they present?

Combinatorial games are games where the complexity arises from the sheer number of possible moves and sequences, rather than strategic depth or psychological elements. Games like chess and Go are examples, and their analysis often requires specialized mathematical tools beyond standard economic game theory due to their high combinatorial complexity.

How does combinatorial game theory differ from traditional game theory in its approach?

Combinatorial game theory focuses on games with perfect information and high complexity, developing unique representations like surreal numbers and using combinatorial and algebraic proof methods. It tackles problems with greater complexity than typically found in economic game theory, sometimes employing non-constructive proofs.

What is the primary distinction between discrete and continuous games?

Discrete games involve a finite number of players, moves, and outcomes. Continuous games, however, allow players to choose strategies from a continuous range of options, such as selecting any non-negative quantity in models like Cournot competition.

What are differential games, and how are their strategies determined?

Differential games are continuous games where the state of the game evolves according to differential equations, often seen in pursuit-evasion scenarios. Optimal strategies for these games are typically found using optimal control theory, such as the Pontryagin maximum principle for open-loop strategies or Bellman's Dynamic Programming for closed-loop strategies.

What is the focus of evolutionary game theory?

Evolutionary game theory studies how strategies change over time based on rules that may not rely on perfect rationality. It models strategy evolution using concepts like Markov chains, often incorporating imitation, optimization, or survival-of-the-fittest dynamics, applicable to both biological and cultural evolution.

How are stochastic outcomes modeled within game theory?

Stochastic outcomes, or random events, can be incorporated into game theory by introducing a "move by nature" player who makes chance moves. This approach allows for the modeling of uncertainty and randomness within the game's structure, similar to how Markov decision processes are used in related fields like AI planning.

What is the difference between the minimax approach and reasoning with probability distributions for stochastic outcomes?

The minimax approach considers the worst-case scenario against an adversary, which can sometimes overestimate unlikely but costly events. Reasoning with probability distributions, as used in methods like Markov Decision Processes, involves calculating expected outcomes based on known probabilities, which might be more appropriate when uncertainty is well-defined.

What are the essential elements required to fully define a game in game theory?

To fully define a game, game theorists must specify the players involved, the information and actions available to each player at every decision point, and the payoffs each player receives for every possible outcome. These elements are sometimes summarized by the acronym PAPI (Players, Actions, Payoffs, Information).

What are the primary forms used to represent non-cooperative games?

Non-cooperative games are typically defined using either the extensive form, which visualizes the game's sequence of moves and information sets, or the normal form, which uses payoff matrices to represent players' strategies and resulting payoffs.

How is the extensive form used to represent games, and what method is used to solve them?

The extensive form represents games with a time sequence of moves using game trees, where vertices denote decision points for players and lines represent actions. To solve these games, backward induction is employed, working backward from the end of the game to determine rational choices at each preceding decision node.

What does the normal form representation of a game typically entail?

The normal form, or strategic form, usually presents a game using a matrix that lists players, their available strategies, and the corresponding payoffs for each outcome. It assumes players act simultaneously or without knowledge of others' moves.

How are cooperative games typically represented in game theory?

Cooperative games are often represented using the characteristic function form. This involves a function that assigns a specific payoff value to every possible coalition of players, indicating the collective benefit they can achieve by cooperating.

How is game theory applied in economics?

In economics, game theory is a primary tool for modeling the behavior of competing entities like firms, markets, and consumers. It's used to analyze phenomena such as auctions, bargaining, mergers, pricing strategies, and market structures like oligopolies and duopolies.

How has game theory been applied to political science?

Game theory is applied in political science to model interactions among voters, interest groups, and politicians. It helps analyze voting behavior, political bargaining, the stability of governments, and phenomena like the "democratic peace," explaining how political structures and outcomes emerge from strategic interactions.

How is game theory utilized in the field of biology?

In biology, game theory, particularly evolutionary game theory, models animal behavior and evolution. Payoffs are often interpreted as biological fitness, and concepts like the evolutionarily stable strategy (ESS) help explain phenomena such as sex ratios, communication, and altruistic behaviors through mechanisms like kin selection.

What role does game theory play in computer science and logic?

Game theory is increasingly important in computer science, underpinning areas like multi-agent systems, artificial intelligence (AI) planning under uncertainty, and the analysis of interactive computations through game semantics. It also provides a basis for algorithmic game theory, which combines computer science and economic theory for problems like auction design and network analysis.

Describe the classic Prisoner's Dilemma scenario and its outcome.

In the Prisoner's Dilemma, two suspects are interrogated separately. Each can either cooperate (stay silent) or betray the other. While mutual cooperation yields a better collective outcome (e.g., shorter sentences), the dominant strategy for each individual is to betray, leading to a suboptimal outcome for both if they both betray.

What is the "Battle of the Sexes" game in game theory, and what are its equilibrium characteristics?

The "Battle of the Sexes" represents a conflict between two players who prefer different outcomes but wish to coordinate their actions. It typically has two pure strategy Nash equilibria where both players choose the same option, and potentially infinite mixed strategy equilibria, reflecting situations where coordination is desired but preferences differ.

Explain the setup and implications of the Ultimatum Game.

In the Ultimatum Game, one player proposes how to split a sum of money with another player, who can either accept or reject the offer. If rejected, both get nothing. This game highlights the influence of fairness, generosity, and social acceptance on economic decisions, often showing behavior that deviates from pure self-interest.

How has game theory been depicted in popular culture, citing specific examples?

Game theory concepts have been featured in films like "A Beautiful Mind," which dramatized John Nash's life and work, and "The Dark Knight," where the Joker presented a Prisoner's Dilemma scenario. The novel and film "Liar Game" also explore game theory problems, and "Crazy Rich Asians" references game theory in its portrayal of strategic decision-making.

What are some of the historically important texts that contributed to the development of game theory?

Historically significant texts include Cournot's "Recherches sur les principes mathématiques de la théorie des richesses" (1838), Zermelo's 1913 paper on chess, von Neumann's 1928 paper and his 1944 book with Morgenstern, "Theory of Games and Economic Behavior," and Luce and Raiffa's "Games and Decisions" (1957).

Game Theory Wiki: The Logic of Strategy: Decoding Game Theory

Dive in with Flashcard Learning!

When you are ready...
🎮 Play the Wiki2Web Clarity Challenge Game🎮

Foundations of Strategic Interaction

Defining Game Theory

Game theory is the rigorous mathematical study of strategic interactions. It provides models to analyze situations where the outcome for each participant depends not only on their own actions but also on the actions of others.¹ Its applications span across numerous disciplines, including economics, logic, systems science, and computer science.²

Evolution of the Field

Initially focused on two-player, zero-sum games (where one player's gain is precisely the other's loss), game theory evolved significantly in the mid-20th century to encompass non-zero-sum games and a broader spectrum of behavioral relationships. It is now considered a fundamental science of rational decision-making across various entities, from humans to artificial intelligence.³

Recognition and Impact

The field's profound impact is underscored by numerous Nobel Memorial Prize in Economic Sciences awarded to game theorists. Its principles are essential for understanding complex systems, from market dynamics to evolutionary processes and political negotiations.¹⁴

Historical Trajectory

Early Seeds

The foundational concepts trace back to the early 18th century with analyses of mixed-strategy solutions, notably the "Waldegrave problem." Later, Antoine Augustin Cournot (1838) presented an early model of oligopoly competition, formalizing what would become known as the Nash equilibrium.⁶ Ernst Zermelo's 1913 work proved that optimal chess strategy is strictly determined.⁸

Formalization and Expansion

John von Neumann is credited with establishing game theory as a distinct field in the early 20th century. His 1928 paper and the seminal 1944 book *Theory of Games and Economic Behavior* (with Oskar Morgenstern) laid the groundwork, introducing concepts like minimax and axiomatic utility theory.⁹¹¹ John Nash significantly advanced the field in the 1950s by developing the Nash equilibrium concept, applicable to a broader range of non-cooperative games.¹⁴

1950s: Development of core concepts like the core, extensive form games, and Shapley value.
1970s: Application to evolutionary biology by John Maynard Smith.
1994: Nash, Selten, and Harsanyi awarded the Nobel Prize for contributions to economic game theory.
2005: Schelling and Aumann recognized for work on dynamic models and correlated equilibria.
2007: Hurwicz, Maskin, and Myerson awarded Nobel for mechanism design theory.
2012: Roth and Shapley recognized for stable allocations and market design.

Foundational Contributions

Key figures like Émile Borel contributed early theorems, while later developments by Reinhard Selten refined solution concepts like subgame perfect equilibria. The field continues to be recognized through prestigious awards, highlighting its enduring relevance.

Classifying Strategic Encounters

Cooperative vs. Non-Cooperative

Games are categorized based on players' ability to form binding agreements. Cooperative games allow for externally enforced commitments, focusing on coalition formation and collective payoffs. Non-cooperative games rely on self-enforcing agreements, analyzing individual strategies and predicting outcomes via concepts like Nash equilibria.¹⁵

Symmetric vs. Asymmetric

A game is symmetric if players receive identical payoffs for identical strategies. Conversely, asymmetric games feature different payoff structures or strategy sets for players, even if the available actions are the same.¹⁸

Zero-Sum vs. Non-Zero-Sum

In zero-sum games, the total gains and losses balance to zero; one player's benefit directly corresponds to another's loss (e.g., poker). Non-zero-sum games allow for outcomes where combined payoffs can be greater or lesser than zero, reflecting potential for mutual gain or loss (e.g., trade negotiations).¹⁹

Simultaneous vs. Sequential

Simultaneous games involve players making decisions without knowledge of the others' current moves, often represented by payoff matrices. Sequential games unfold over time, with players making decisions based on knowledge of previous actions, typically visualized using game trees.²⁰

Information Sets

Games differ in the information available to players. Perfect information games (e.g., chess) allow players to know all prior moves. Imperfect information games (e.g., poker) involve uncertainty about opponents' actions, often modeled using information sets.²¹ Bayesian games specifically address situations with incomplete information about player characteristics.²⁹

Other Classifications

Game theory also encompasses combinatorial games (complex move structures like Go), continuous games (continuous strategy choices), differential games (strategies evolving based on differential equations), and evolutionary game theory (modeling strategy evolution based on non-rational adaptation).³¹

Frameworks for Analysis

Extensive Form

This representation visualizes games using decision trees, mapping out players, their decision points (nodes), available actions (branches), and final payoffs. It's crucial for analyzing sequential moves and requires backward induction for solving.⁴⁷

The extensive form can also represent simultaneous moves and imperfect information using dotted lines to denote information sets.

Normal Form

The normal (or strategic) form uses matrices to represent games, detailing players, their strategies, and resulting payoffs. It's typically used for simultaneous-move games. While equivalent to the extensive form, conversion can lead to significant size increases.⁴⁹

	Player 2 chooses Left	Player 2 chooses Right
Player 1 chooses Up	4, 3	–1, –1
Player 1 chooses Down	0, 0	3, 4
Normal form payoff matrix

This matrix illustrates payoffs for Player 1 (row) and Player 2 (column) based on their choices.

Characteristic Function Form

Primarily used in cooperative game theory, this form defines the payoff achievable by each possible coalition (subset) of players. It specifies the value v(S) for every coalition S, where v(∅) = 0.⁵⁰

Ubiquitous Applications

Economics & Business

Game theory is fundamental to modeling market behaviors, including auctions, bargaining, pricing strategies, mergers, and industrial organization. It helps analyze firm competition, cooperation, and strategic decision-making in various business contexts.^c¹⁰⁷

Political Science

Researchers apply game theory to understand voting behavior, political economy, public choice, war bargaining, and the stability of governments. Models often involve players like voters, states, and politicians, analyzing strategic interactions in policy-making and international relations.¹¹¹

Biology & Evolution

In biology, payoffs often represent fitness. Evolutionary game theory uses concepts like the Evolutionarily Stable Strategy (ESS) to model animal behavior, the stability of sex ratios, biological altruism (kin selection), and fighting strategies.⁶⁸¹²¹

Computer Science & AI

Game theory underpins multi-agent systems, artificial intelligence, machine learning algorithms (like reinforcement learning), and network protocols. It's crucial for designing autonomous systems, analyzing online algorithms, and understanding security vulnerabilities.¹²⁴

Philosophy & Ethics

Philosophers utilize game theory to analyze conventions, social norms, meaning, and interactive epistemology. It informs discussions on morality, self-interest, and the foundations of social contracts, tracing back to thinkers like Plato and Hobbes.¹³³

Defence & Project Management

Applications extend to defense strategy (cybersecurity, resource allocation) and project management, modeling interactions between stakeholders like investors, contractors, and government entities to optimize decision-making and manage complex interdependencies.¹¹⁸¹⁰⁷

Illustrative Games

Prisoner's Dilemma

Two suspects face separate interrogations. Mutual cooperation (silence) yields a lighter sentence (-2 years each) than mutual betrayal (-5 years each). However, betraying the other while they remain silent yields freedom (0 years) for the betrayer, while the silent one gets a severe sentence (-10 years). The dominant strategy is to betray, leading to a suboptimal outcome for both.¹⁴⁵

Prisoner's Dilemma Payoffs
	B Stays Silent	B Betrays
A Stays Silent	-2, -2	-10, 0
A Betrays	0, -10	-5, -5

Battle of the Sexes

A couple must decide between attending a concert or a football match. Both prefer to attend together, but have different preferences for the event. This coordination game has two pure strategy Nash equilibria (both attend concert, or both attend football) and illustrates the challenge of coordinating preferences.¹⁴⁷

Ultimatum Game

One player proposes a split of a sum of money; the other accepts or rejects. Acceptance yields the proposed split; rejection results in nothing for both. This game highlights fairness and social norms, as responders often reject extremely unfair offers, deviating from purely rational self-interest.¹⁴⁹

Trust Game

An investor decides how much to send to a trustee, which is then tripled. The trustee decides how much to return. Experiments show people often place trust (send money) expecting reciprocity, demonstrating the role of trust beyond pure self-interest.¹⁵¹

Cournot Competition

Firms simultaneously choose production quantities for a homogeneous product. Each firm aims to maximize profit based on expected competitor output. The equilibrium occurs when firms produce quantities that are best responses to each other, often leading to lower prices than monopoly.²¹

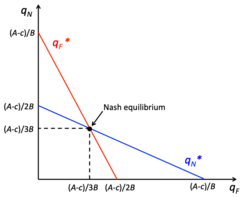
Bertrand Competition

Firms compete by setting prices for homogeneous products. The equilibrium typically drives prices down to marginal cost, as firms undercut each other to capture the entire market.²¹

Game Theory in the Cultural Sphere

Cinematic and Literary Depictions

Game theory concepts frequently appear in popular culture. The life of John Nash was depicted in the film *A Beautiful Mind*. Movies like *Dr. Strangelove* satirize deterrence theory, while *The Dark Knight* famously illustrated the Prisoner's Dilemma. The manga and series *Liar Game* centers around game theory challenges.¹⁵⁵¹⁵⁸¹⁶⁰

Musical Influence

The band "Game Theory" took its name from the field, reflecting its focus on strategic thinking and minimizing failure.¹⁵⁹

Literary Explorations

Robert Heinlein's *Starship Troopers* referenced "games theory." Len Deighton's *Spy Story* explored game theory in Cold War contexts. Liu Cixin's *The Dark Forest* uses game theory to explore potential extraterrestrial interactions.¹⁵⁷

Teacher's Corner

Edit and Print this course in the Wiki2Web Teacher Studio

Edit and Print Materials from this study in the wiki2web studio

Click here to open the "Game Theory" Wiki2Web Studio curriculum kit

Use the free Wiki2web Studio to generate printable flashcards, worksheets, exams, and export your materials as a web page or an interactive game.

True or False?

Test Your Knowledge!

Gamer's Corner

Are you ready for the Wiki2Web Clarity Challenge?

Learn about game_theory while playing the wiki2web Clarity Challenge game.

Unlock the mystery image and prove your knowledge by earning trophies. This simple game is addictively fun and is a great way to learn!

Play now

Explore More Topics

Discover other topics to study!

hollywood forever cemetery

exoplanet

butterfly roof

george abe

References

For a more detailed discussion of the use of game theory in ethics, see the Stanford Encyclopedia of Philosophy's entry game theory and ethics.

Edgeworth, Francis (1889) "The pure theory of monopoly", reprinted in Collected Papers relating to Political Economy 1925, vol.1, Macmillan.

Martin Shubik (1978). "Game Theory: Economic Applications," in W. Kruskal and J.M. Tanur, ed., International Encyclopedia of Statistics, v. 2, pp. 372â78.

A full list of references for this article are available at the Game theory Wikipedia page

Feedback & Support

To report an issue with this page, or to find out ways to support the mission, please click here.

Academic Disclaimer

Important Notice

This content has been generated by an AI model and is intended for educational and informational purposes only. It is based on data synthesized from publicly available sources, primarily Wikipedia, and may not represent the most current or complete understanding of the subject matter.

This is not professional advice. The information provided does not constitute expert consultation in economics, mathematics, political science, or any other field. Readers should consult with qualified professionals for specific applications or advice. Reliance on any information provided here is solely at your own risk.

The creators of this page are not liable for any errors, omissions, or consequences arising from the use of this information.

The Logic of Strategy

💡 Dive in with Flashcard Learning! 💡

Foundations of Strategic Interaction ♟️

🧠 Defining Game Theory

⚖️ Evolution of the Field

🏆 Recognition and Impact

Historical Trajectory ⏳

📜 Early Seeds

🚀 Formalization and Expansion

💡 Foundational Contributions

Classifying Strategic Encounters 📊

🤝 Cooperative vs. Non-Cooperative

⚖️ Symmetric vs. Asymmetric

+/- Zero-Sum vs. Non-Zero-Sum

⏱️ Simultaneous vs. Sequential

❓ Information Sets

🧩 Other Classifications

Frameworks for Analysis 📐

🌳 Extensive Form

🔢 Normal Form

🧮 Characteristic Function Form

Ubiquitous Applications 🌍

💰 Economics & Business

🏛️ Political Science

🌱 Biology & Evolution

💻 Computer Science & AI

🤔 Philosophy & Ethics

🛡️ Defence & Project Management

Illustrative Games 🎲

🤝 Prisoner's Dilemma

🎭 Battle of the Sexes

⚖️ Ultimatum Game

🤝 Trust Game

🏭 Cournot Competition

🏷️ Bertrand Competition

Game Theory in the Cultural Sphere 🎬

🎬 Cinematic and Literary Depictions

🎵 Musical Influence

📚 Literary Explorations

Teacher's Corner 🧑‍🏫

Edit and Print this course in the Wiki2Web Teacher Studio

True or False? 🤔

❓ Test Your Knowledge! ❓

Gamer's Corner 🎮

Are you ready for the Wiki2Web Clarity Challenge?

Explore More Topics

📜 Discover other topics to study!

References

📜 References

Feedback & Support 👍

To report an issue with this page, or to find out ways to support the mission, please click here.

Academic Disclaimer ⚠️

📜 Important Notice

Dive in with Flashcard Learning!

Foundations of Strategic Interaction

Defining Game Theory

Evolution of the Field

Recognition and Impact

Historical Trajectory

Early Seeds

Formalization and Expansion

Foundational Contributions

Classifying Strategic Encounters

Cooperative vs. Non-Cooperative

Symmetric vs. Asymmetric

Zero-Sum vs. Non-Zero-Sum

Simultaneous vs. Sequential

Information Sets

Other Classifications

Frameworks for Analysis

Extensive Form

Normal Form

Characteristic Function Form

Ubiquitous Applications

Economics & Business

Political Science

Biology & Evolution

Computer Science & AI

Philosophy & Ethics

Defence & Project Management

Illustrative Games

Prisoner's Dilemma

Battle of the Sexes

Ultimatum Game

Trust Game

Cournot Competition

Bertrand Competition

Game Theory in the Cultural Sphere

Cinematic and Literary Depictions

Musical Influence

Literary Explorations

Teacher's Corner

True or False?

Test Your Knowledge!

Gamer's Corner

Discover other topics to study!

References

Feedback & Support

Academic Disclaimer

Important Notice