What is the fundamental definition of a group homomorphism?

A group homomorphism is a function, denoted as h, between two groups, (G, *) and (H, ·), that preserves the group operation. This means that for any elements u and v in group G, the equation h(u * v) = h(u) · h(v) must hold true, where * is the operation in G and · is the operation in H.

How does a group homomorphism relate the identity elements of the two groups it maps between?

A group homomorphism always maps the identity element of the first group (G) to the identity element of the second group (H). If e_G is the identity in G and e_H is the identity in H, then the homomorphism h satisfies h(e_G) = e_H.

What property does a group homomorphism exhibit concerning the inverses of elements?

A group homomorphism maps the inverse of an element in the domain group to the inverse of the image of that element in the codomain group. Specifically, for any element u in G, the homomorphism h satisfies h(u⁻¹) = h(u)⁻¹.

What does it mean for a function to be 'compatible with the group structure' in the context of group homomorphisms?

A function is considered 'compatible with the group structure' if it respects the group operation. For a group homomorphism, this compatibility is demonstrated by the property that applying the function to the product of two elements in the source group yields the same result as taking the product of their images in the target group.

What is a monomorphism in the context of group homomorphisms?

A monomorphism is a group homomorphism that is injective, meaning it maps distinct elements of the domain group to distinct elements of the codomain group. In other words, if h(u) = h(v), then it must be that u = v.

Define an epimorphism as a type of group homomorphism.

An epimorphism is a group homomorphism that is surjective, meaning that every element in the codomain group (H) is the image of at least one element from the domain group (G). Essentially, the homomorphism covers the entire codomain.

What characterizes a group isomorphism?

A group isomorphism is a group homomorphism that is bijective, meaning it is both injective (a monomorphism) and surjective (an epimorphism). Isomorphic groups are structurally identical and differ only in the notation of their elements; their inverse function is also a group homomorphism.

What is an endomorphism of a group?

An endomorphism is a group homomorphism where the domain and the codomain are the same group. It is a function h: G → G that preserves the group structure.

What is an automorphism of a group?

An automorphism is an endomorphism that is also an isomorphism. It is a bijective homomorphism from a group onto itself, preserving the group's structure while potentially rearranging its elements.

What algebraic structure does the set of all automorphisms of a group form?

The set of all automorphisms of a group G, when equipped with the operation of functional composition, forms a group itself. This group is known as the automorphism group of G and is denoted by Aut(G).

How is the kernel of a group homomorphism defined?

The kernel of a group homomorphism h from group G to group H, denoted as ker(h), is the set of all elements in G that are mapped by h to the identity element of H. Mathematically, it is expressed as ker(h) = {u ∈ G | h(u) = e_H}, where e_H is the identity element of H.

How is the image of a group homomorphism defined?

The image of a group homomorphism h: G → H, denoted as im(h) or h(G), is the set of all elements in H that are the result of applying h to elements in G. It is formally defined as im(h) = {h(u) | u ∈ G}.

What is the relationship between the image of a homomorphism and the codomain group?

The image of a group homomorphism is always a subgroup of the codomain group. It represents the subset of the codomain that is 'reached' or 'covered' by the homomorphism.

What type of subgroup is the kernel of a group homomorphism?

The kernel of a group homomorphism is always a normal subgroup of the domain group. This means that for any element u in the kernel and any element g in the domain group, the conjugate g⁻¹ * u * g is also in the kernel.

What does the first isomorphism theorem state about the image of a group homomorphism?

The first isomorphism theorem states that the image of a group homomorphism h (i.e., h(G)) is isomorphic to the quotient group formed by dividing the domain group G by its kernel (G/ker h). This theorem establishes a fundamental connection between homomorphisms, kernels, images, and quotient groups.

Under what specific condition is a group homomorphism injective (a monomorphism)?

A group homomorphism h is injective if and only if its kernel contains only the identity element of the domain group. In other words, ker(h) = {e_G}, where e_G is the identity element of G.

Provide an example of a group homomorphism involving the cyclic group Z₃.

Consider the map h: Z → Z /3 Z defined by h(u) = u mod 3. This function is a group homomorphism because it preserves the addition operation. It is surjective, and its kernel consists of all integers divisible by 3.

Describe the exponential map as a homomorphism between the additive group of complex numbers and the multiplicative group of non-zero complex numbers.

The exponential map also acts as a group homomorphism from the additive group of complex numbers ( C , +) to the multiplicative group of non-zero complex numbers ( C *, ·). This map is surjective, and its kernel is the set of all integer multiples of 2πi, {2πki | k ∈ Z }.

What is the relationship between group homomorphisms and the category of groups?

Group homomorphisms serve as the morphisms (structure-preserving maps) in the category of groups. This means that the collection of all groups, with group homomorphisms as the arrows connecting them, forms a mathematical category known as the category of groups.

How is the set of homomorphisms between two abelian groups structured?

When G and H are abelian groups, the set of all group homomorphisms from G to H, denoted Hom(G, H), forms an abelian group itself. This is achieved by defining the sum of two homomorphisms, (h + k), pointwise: (h + k)(u) = h(u) + k(u) for all elements u in G.

What property of the codomain group is necessary for the sum of two homomorphisms to also be a homomorphism?

The commutativity (or abelian property) of the codomain group H is essential to ensure that the sum of two homomorphisms, h + k, is also a valid group homomorphism. This property allows for the necessary rearrangement of terms to prove the homomorphism property for the sum.

What is the endomorphism ring of an abelian group?

The endomorphism ring of an abelian group G is formed by the set of all endomorphisms (homomorphisms from G to itself), equipped with operations of pointwise addition and functional composition. This structure arises because the composition of homomorphisms is compatible with their addition.

What is the endomorphism ring of the direct sum of m copies of Z/nZ isomorphic to?

The endomorphism ring of the direct sum of m copies of the cyclic group Z/nZ is isomorphic to the ring of m-by-m matrices whose entries are elements of Z/nZ. This demonstrates a concrete link between group theory and matrix algebra.

What mathematical structure does the category of abelian groups represent?

The category of abelian groups, with homomorphisms as morphisms and well-behaved direct sums and kernels, is a prime example of an abelian category. This classification signifies that it possesses properties allowing for advanced algebraic constructions and theorems.

What is the defining characteristic of a homomorphism in terms of preserving structure?

A homomorphism preserves the algebraic structure of the groups it maps between. This means it respects the group operation, ensuring that the result of an operation in the source group corresponds to the operation on the images in the target group.

What is the kernel of the homomorphism Φ(x) = √2 * x from (Z, +) to (R, +)?

The kernel of the homomorphism Φ(x) = √2 * x from the group of integers (Z, +) to the group of real numbers (R, +) is the set of integers that map to the identity element (0) in R. Since √2 is non-zero, the only integer x for which √2 * x = 0 is x = 0. Thus, the kernel is {0}.

What is the image of the homomorphism Φ(x) = √2 * x from (Z, +) to (R, +)?

The image of the homomorphism Φ(x) = √2 * x from (Z, +) to (R, +) is the set of all real numbers that are integer multiples of the square root of 2. This set can be represented as {k√2 | k ∈ Z}.

What is the kernel of the exponential map from (C, +) to (C*, *)?

The kernel of the exponential map from the additive group of complex numbers (C, +) to the multiplicative group of non-zero complex numbers (C*, *) is the set of complex numbers that map to the identity element (1) in C*. This kernel is precisely the set of all integer multiples of 2πi, denoted as {2πki | k ∈ Z}.

What is the image of the exponential map from (R, +) to (R*, *)?

The image of the exponential map exp(x) = eˣ, which maps the additive group of real numbers (R, +) to the multiplicative group of non-zero real numbers (R*, *), is the set of all positive real numbers. This is because the exponential function always yields positive outputs for real inputs.

What is the relationship between the composition of homomorphisms and the structure of the category of groups?

The composition of two group homomorphisms is itself a group homomorphism. This property is fundamental to the definition of a category, where homomorphisms act as morphisms, and their composition allows for the study of relationships and structures within the category of groups.

What is the significance of the term 'isomorphic' when comparing two groups?

When two groups are described as isomorphic, it means they are structurally identical. There exists a bijective homomorphism (an isomorphism) between them, indicating that they share the same fundamental algebraic properties, even if their elements are named differently.

What is the definition of a monomorphism in group theory?

A monomorphism in group theory is a group homomorphism that is injective, meaning it maps distinct elements of the domain group to distinct elements of the codomain group.

What is the definition of an epimorphism in group theory?

An epimorphism in group theory is a group homomorphism that is surjective, meaning that every element in the codomain group is the image of at least one element from the domain group.

What is the kernel of the homomorphism h(u) = u mod 3 from (Z, +) to (Z₃, +)?

The kernel of the homomorphism h(u) = u mod 3 from the group of integers (Z, +) to the cyclic group Z₃ (with addition modulo 3) is the set of all integers that are divisible by 3. These are the integers that map to 0, the identity element in Z₃.

What is the image of the homomorphism h(u) = u mod 3 from (Z, +) to (Z₃, +)?

The image of the homomorphism h(u) = u mod 3 from (Z, +) to (Z₃, +) is the entire group Z₃, which consists of the elements {0, 1, 2}. This is because every element in Z₃ can be obtained by taking an integer modulo 3.

What is the relationship between the kernel of a homomorphism and the concept of injectivity?

A group homomorphism is injective if and only if its kernel consists solely of the identity element of the domain group. If the kernel contains any non-identity elements, those elements are mapped to the identity, meaning distinct elements are mapped to the same element, thus violating injectivity.

What is the definition of a group homomorphism in terms of mapping elements?

A group homomorphism is a function h from group G to group H such that for any two elements u and v in G, the image of their product (u * v) under h is equal to the product of their individual images, h(u) · h(v).

What is the significance of the term 'compatible with the group structure' when referring to a homomorphism?

When a function is described as 'compatible with the group structure,' it means that the function respects the underlying operation of the group. For group homomorphisms, this compatibility is precisely captured by the property h(u * v) = h(u) · h(v).

What is the kernel of a homomorphism, and what does it represent in terms of group structure?

The kernel of a homomorphism h: G → H is the set of elements in G that are mapped to the identity element of H. It represents the 'null space' of the homomorphism, indicating which elements of G are collapsed to the identity in H.

What is the image of a homomorphism, and how does it relate to the structure of the codomain?

The image of a homomorphism h: G → H is the set of all elements in H that are the result of applying h to elements in G. It represents the portion of the codomain group that is 'covered' by the homomorphism and is always a subgroup of H.

What is the condition for a group homomorphism to be an automorphism?

A group homomorphism is an automorphism if it is a bijective map from a group to itself. This means it must be both injective (one-to-one) and surjective (onto), preserving the group structure while rearranging its elements.

What is the definition of an endomorphism?

An endomorphism is a homomorphism where the domain and codomain are the same group. It's a structure-preserving map from a group onto itself.

What is the automorphism group of the cyclic group of integers (Z, +)?

The automorphism group of the cyclic group of integers (Z, +) consists of only two elements: the identity transformation and multiplication by -1. This group is isomorphic to Z/2Z, the cyclic group of order 2.

What is the relationship between the composition of homomorphisms and the category of groups?

The composition of two group homomorphisms is itself a group homomorphism. This property is fundamental to the definition of a category, where homomorphisms act as morphisms, and their composition allows for the study of relationships and structures within the category of groups.

What is the structure formed by the set of homomorphisms between two abelian groups?

The set of homomorphisms between two abelian groups forms an abelian group itself, with the operation of addition defined pointwise. This means that for any two homomorphisms h and k, their sum (h+k) is defined by (h+k)(u) = h(u) + k(u) for all elements u in the domain group.

What is the definition of a group homomorphism in terms of the group operation?

A group homomorphism is a function h between two groups, G and H, such that for any elements u and v in G, the equation h(u * v) = h(u) · h(v) holds true, where * denotes the operation in G and · denotes the operation in H.

What is the kernel of a homomorphism, and why is it important?

The kernel of a homomorphism h: G → H is the set of elements in G that map to the identity element of H. It is important because it measures how far the homomorphism is from being injective, and it is always a normal subgroup of G.

What is the image of a homomorphism, and what property does it have in the codomain group?

The image of a homomorphism h: G → H is the set of all elements in H that are mapped to by elements of G. It represents the portion of the codomain group that is 'covered' by the homomorphism and is always a subgroup of H.

What is the condition for a group homomorphism to be an automorphism?

A group homomorphism is an automorphism if it is a bijective map from a group to itself. This means it must be both injective (one-to-one) and surjective (onto), preserving the group structure while rearranging its elements.

What is the definition of an endomorphism?

An endomorphism is a homomorphism where the domain and codomain are the same group. It's a structure-preserving map from a group onto itself.

Group Homomorphism Wiki: Algebraic Bridges: Understanding Group Homomorphisms

Dive in with Flashcard Learning!

When you are ready...
🎮 Play the Wiki2Web Clarity Challenge Game🎮

What is a Group Homomorphism?

Preserving Structure

In mathematics, specifically within abstract algebra, a group homomorphism is a function between two groups that respects their algebraic structure. Given two groups, (G, \u2217) and (H, \u00b7), a function h: G \u2192 H is a group homomorphism if, for all elements u and v in G, the following property holds:

h(u*v)=h(u)\cdot h(v)

This means that applying the operation in group G first and then mapping the result to H yields the same outcome as mapping the elements u and v to H first and then applying the operation in H.

Fundamental Properties

From the defining property, several key characteristics of group homomorphisms can be derived:

A homomorphism h maps the identity element of G (denoted e_G) to the identity element of H (denoted e_H):
$h(e_{G})=e_{H}$ $h(e_{G})=e_{H}$
Homomorphisms preserve inverses: for any element u in G, the image of its inverse is the inverse of its image in H.
$h\left(u^{-1}\right)=h(u)^{-1}.\,$ $h\left(u^{-1}\right)=h(u)^{-1}.\,$

These properties collectively indicate that a homomorphism is compatible with the group operations and structure.

Visualizing the Concept

Imagine mapping elements from one group (G) to another (H). A homomorphism ensures that the relationship (the group operation) between any two elements in G is mirrored by the relationship between their corresponding images in H. The provided diagram illustrates this: the structure of operations in G is preserved in H through the mapping h.

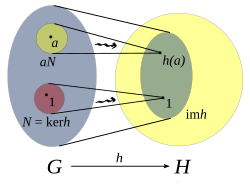
The diagram shows how elements from G are mapped to H. The set of elements in G that map to the identity element in H forms the kernel (N), which is a normal subgroup. The set of all images of elements from G in H constitutes the image of the homomorphism.

Key Properties

Identity and Inverses

As previously noted, a homomorphism h: G \u2192 H always maps the identity element of G to the identity element of H ( $h(e_{G})=e_{H}$ $h(e_{G})=e_{H}$ ). It also preserves the inverse relationship: $h(u^{-1})=h(u)^{-1}$ $h(u^{-1})=h(u)^{-1}$

These properties are direct consequences of the homomorphism definition and the axioms of group theory.

Image and Kernel

Two crucial sets associated with a homomorphism h: G \u2192 H are:

The kernel, denoted ker(h), is the set of elements in G that map to the identity element in H:
$\operatorname {ker} (h):=\left\{u\in G\colon h(u)=e_{H}\right\}.$ $\operatorname {ker} (h):=\left\{u\in G\colon h(u)=e_{H}\right\}.$
The image, denoted im(h) or h(G), is the set of all elements in H that are mapped to by some element in G:
$\operatorname {im} (h):=h(G)\equiv \left\{h(u)\colon u\in G\right\}.$ $\operatorname {im} (h):=h(G)\equiv \left\{h(u)\colon u\in G\right\}.$

The kernel is always a normal subgroup of G, and the image is always a subgroup of H. The relationship between these sets is fundamental, as formalized by the First Isomorphism Theorem, which states that G/ker(h) is isomorphic to im(h).

Classifying Homomorphisms

Monomorphism

A group homomorphism h: G \u2192 H is a monomorphism if it is injective (one-to-one). This occurs precisely when the kernel contains only the identity element of G, i.e., ker(h) = {e_G}.

Injectivity ensures that distinct elements in G map to distinct elements in H. The condition ker(h) = {e_G} is equivalent to injectivity because if h(g₁) = h(g₂), then h(g₁g₂^-1) = e_H. If the kernel is trivial, this implies g₁g₂^-1 = e_G, which means g₁ = g₂.

Epimorphism

A group homomorphism h: G \u2192 H is an epimorphism if it is surjective (onto). This means that every element in H is the image of at least one element in G.

Surjectivity implies that the image of the homomorphism is the entire codomain group H (im(h) = H). This is a strong condition, indicating that the homomorphism "covers" all elements of the target group.

Isomorphism

A group homomorphism h: G \u2192 H is an isomorphism if it is both injective and surjective (i.e., bijective). If an isomorphism exists between two groups, they are considered isomorphic, meaning they are structurally identical, differing only in the notation of their elements.

An isomorphism implies a perfect structural correspondence. The inverse function h^-1: H \u2192 G is also a group homomorphism. Isomorphic groups share all their algebraic properties.

Endomorphism and Automorphism

An endomorphism is a homomorphism from a group to itself (h: G \u2192 G). An automorphism is an endomorphism that is also an isomorphism. The set of all automorphisms of a group G forms a group under function composition, known as the automorphism group, Aut(G).

For example, the group of integers under addition (Z, +) has only two automorphisms: the identity map and the map that sends x to -x. This automorphism group is isomorphic to the cyclic group of order 2, Z/2Z.

Illustrative Examples

Cyclic Group Example

Consider the cyclic group Z₃ = ({0, 1, 2}, +) and the group of integers (Z, +). The map h: Z \u2192 Z₃ defined by h(u) = u mod 3 is a group homomorphism. It is surjective, and its kernel is the set of all multiples of 3, {..., -6, -3, 0, 3, 6, ...}.

Exponential Map

The exponential map provides a homomorphism from the additive group of real numbers (R, +) to the multiplicative group of non-zero real numbers (R⁺, \u00b7). The function f(x) = e^x satisfies f(x + y) = e^x+y = e^xe^y = f(x)\u00b7f(y). This map is injective, with kernel {0}. Similarly, for complex numbers, the map f(z) = e^z is a homomorphism from (C, +) to (C*, \u00b7), with kernel {2\u03c0ki | k \u2208 Z}.

Logarithm Function

The logarithm function serves as a homomorphism from the multiplicative group of positive real numbers (R⁺, \u00b7) to the additive group of real numbers (R, +). The property log(ab) = log(a) + log(b) directly demonstrates the homomorphism property.

Matrix Group Example

Consider the group G of matrices of the form $\left\{{\begin{pmatrix}a&b\\0&1\end{pmatrix}}{\bigg |}a>0,b\in \mathbf {R} \right\}$ $\left\{{\begin{pmatrix}a&b\\0&1\end{pmatrix}}{\bigg |}a>0,b\in \mathbf {R} \right\}$

under matrix multiplication. For any complex number u, the function f_u: G \u2192 C^* defined by $\left({\begin{smallmatrix}a&b\\0&1\end{smallmatrix}}\right)\mapsto a^{u}$ $\left({\begin{smallmatrix}a&b\\0&1\end{smallmatrix}}\right)\mapsto a^{u}$

This mapping preserves the matrix multiplication structure and is thus a group homomorphism. The specific value of u determines the nature of the homomorphism.

Category Theory Perspective

The Category of Groups

The collection of all groups, with group homomorphisms as the structure-preserving maps (morphisms), forms a fundamental structure in mathematics known as the category of groups (often denoted Grp). If h: G \u2192 H and k: H \u2192 K are group homomorphisms, their composition (k \u2218 h): G \u2192 K is also a group homomorphism. This composition property is essential for defining a category.

Homomorphisms of Abelian Groups

Structure of Homomorphisms

When dealing with abelian groups (where the group operation is commutative), the set of all homomorphisms between two such groups, Hom(G, H), forms an abelian group itself. The addition of two homomorphisms, h and k, is defined pointwise: (h + k)(u) = h(u) + k(u) for all u \u2208 G. The commutativity of H is crucial for proving that h + k is also a homomorphism.

This additive structure, combined with composition, allows for the definition of an endomorphism ring End(G) for an abelian group G. For instance, the endomorphism ring of a direct sum of m copies of Z/nZ is isomorphic to the ring of mxm matrices with entries from Z/nZ. This structure makes the category of abelian groups a foundational example of an abelian category.

Related Concepts

Key Connections

Homomorphism: The general concept applicable to various algebraic structures.
Fundamental Theorem on Homomorphisms: Establishes the isomorphism G/ker(h) \u2191 im(h).
Ring Homomorphism: Preserves the structure of rings, which involve both addition and multiplication.
Category Theory: Provides the abstract framework for studying mathematical structures and their relationships, where groups and homomorphisms are central objects.

Teacher's Corner

Edit and Print this course in the Wiki2Web Teacher Studio

Edit and Print Materials from this study in the wiki2web studio

Click here to open the "Group Homomorphism" Wiki2Web Studio curriculum kit

Use the free Wiki2web Studio to generate printable flashcards, worksheets, exams, and export your materials as a web page or an interactive game.

True or False?

Test Your Knowledge!

Gamer's Corner

Are you ready for the Wiki2Web Clarity Challenge?

Learn about group_homomorphism while playing the wiki2web Clarity Challenge game.

Unlock the mystery image and prove your knowledge by earning trophies. This simple game is addictively fun and is a great way to learn!

Play now

Explore More Topics

Discover other topics to study!

commercial revolution

condorcet winner criterion

mainz

References

A full list of references for this article are available at the Group homomorphism Wikipedia page

Feedback & Support

To report an issue with this page, or to find out ways to support the mission, please click here.

Disclaimer

Important Notice

This page was generated by an Artificial Intelligence and is intended for informational and educational purposes only. The content is based on a snapshot of publicly available data from Wikipedia and may not be entirely accurate, complete, or up-to-date.

This is not mathematical advice. The information provided on this website is not a substitute for professional mathematical consultation, study, or verification. Always refer to authoritative textbooks, academic resources, and qualified instructors for a thorough understanding of abstract algebra concepts.

The creators of this page are not responsible for any errors or omissions, or for any actions taken based on the information provided herein.

Algebraic Bridges

💡 Dive in with Flashcard Learning! 💡

What is a Group Homomorphism? 🔗

➡️ Preserving Structure

⭐ Fundamental Properties

🖼️ Visualizing the Concept

Key Properties ⭐

🔑 Identity and Inverses

➿ Image and Kernel

Classifying Homomorphisms 🏷️

➡️ Monomorphism

⬆️ Epimorphism

⚖️ Isomorphism

🔄 Endomorphism and Automorphism

Illustrative Examples 💡

➕ Cyclic Group Example

📈 Exponential Map

√ Logarithm Function

🧮 Matrix Group Example

Category Theory Perspective 🏗️

📦 The Category of Groups

Homomorphisms of Abelian Groups ➕

➕ Structure of Homomorphisms

Related Concepts 📚

🔗 Key Connections

Teacher's Corner 🧑‍🏫

Edit and Print this course in the Wiki2Web Teacher Studio

True or False? 🤔

❓ Test Your Knowledge! ❓

Gamer's Corner 🎮

Are you ready for the Wiki2Web Clarity Challenge?

Explore More Topics

📜 Discover other topics to study!

References

📜 References

Feedback & Support 👍

To report an issue with this page, or to find out ways to support the mission, please click here.

Disclaimer ⚠️

📜 Important Notice

Dive in with Flashcard Learning!

What is a Group Homomorphism?

Preserving Structure

Fundamental Properties

Visualizing the Concept

Key Properties

Identity and Inverses

Image and Kernel

Classifying Homomorphisms

Monomorphism

Epimorphism

Isomorphism

Endomorphism and Automorphism

Illustrative Examples

Cyclic Group Example

Exponential Map

Logarithm Function

Matrix Group Example

Category Theory Perspective

The Category of Groups

Homomorphisms of Abelian Groups

Structure of Homomorphisms

Related Concepts

Key Connections

Teacher's Corner

True or False?

Test Your Knowledge!

Gamer's Corner

Discover other topics to study!

References

Feedback & Support

Disclaimer

Important Notice